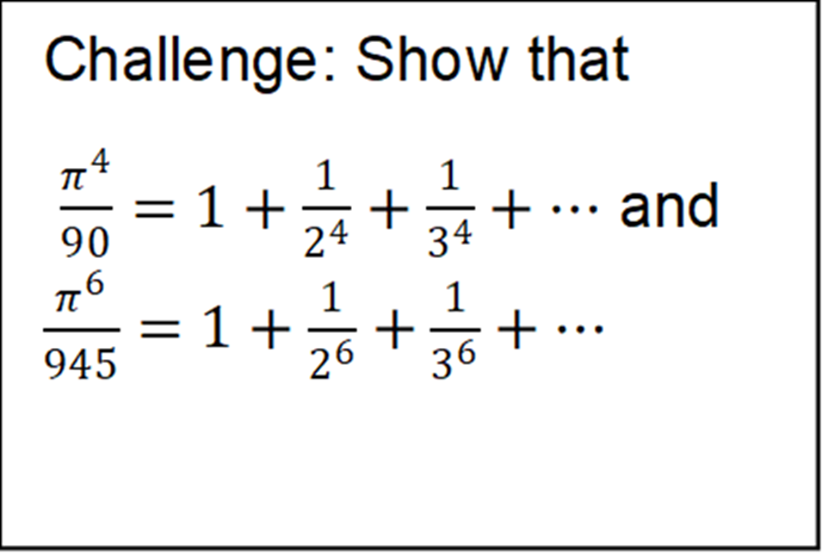Suggested Level: Advanced High School Senior and up
Solutions to Challenges in this topic are here:
All numbers are made up of prime numbers. Prime numbers are the atoms of arithmetic, since every number can be written uniquely as a product of primes. We know that there are an infinite number of primes, but where are they? Are there huge regions of numerical space in which no primes are present at all? And are there other regions where large numbers of primes are concentrated? The Riemann Hypothesis is a conjecture about how the prime numbers are distributed throughout the infinite space of numbers. It answers the question, “How many primes are there less than or equal to some given number?” If we could answer that question as precisely as possible, the result would obviously have very important implications for our understanding of the numbers. Because the answer would tell us so much about the numbers, the Riemann Hypothesis is considered to be the most important unsolved problem in pure mathematics. Over 500 mathematical results have been proved to be true if the Riemann Hypothesis is true. Fame and fortune awaits anyone who can resolve the Riemann Hypothesis. The Riemann Hypothesis was the 8th of Hilbert’s 23 challenge problems and is also one of the Clay Mathematics Institute’s 7 millennium prize problems, with a $1 million prize for its proof.
Early Attempts To Understand the Distribution of Prime Numbers
Can we find a formula to predict the distribution of prime numbers? This is the question that the mathematician Karl Frederick Gauss turned to in his youth.
Karl Frederick Gauss
Called the “Prince of Mathematics,” Gauss made profound discoveries in many areas of mathematics, many of which he never published. For example, he discovered non-Euclidean geometry that would later be used in General Relativity. His motto regarding his mathematical research was: “Pauca, sed matura—Few, but ripe.” Besides mathematics, he was very good at languages and by 19 had already mastered German, English, Greek, Latin, Danish, and French. Later in life he also mastered Russian and Swedish. He called mathematics the “Queen of the Sciences” and number theory the “Queen of Mathematics.” As a boy, Gauss was obsessed with prime numbers and spent his free time calculating them.
From calculating prime numbers, Gauss observed that they thinned out according to a pattern. We can see how prime numbers thin out by graphing the Prime Counting Function.
The Prime Counting Function
For any number N, the prime counting function counts the exact number of primes less than or equal to N. For example, if we wanted to know the number of primes less than or equal to 100, we’d feed 100 to the prime counting function and get 25. The Prime Counting function looks like a staircase since for some numbers we don’t have any more primes than we did for previous numbers. For example, there are 6 primes up to and including the number 13: 2,3,5,7,11,and 13. So, if we feed 13 to the prime counting function, we get 6. But since 14,15, and 16 are not prime, we also get 6 if we feed 14, 15, or 16 to the function.
Gauss observed that the probability of selecting a prime at random from numbers 2 to N is approximately 1/ln(N). It’s as if Nature is throwing a Log-weighted coin. The expected number of primes between 2 and N would then be N/ln(N) As seen in the chart below, Gauss’s approximation seems to underestimate the true number of primes.
Gauss refined his estimate of the number of primes that are less than or equal to some number N by noting that a better approximation is
A key step that Gauss took, which brings to bear the tools of calculus to solve questions in number theory, was to write the approximation as an integral, the logarithmic integral function, denoted li(N) and defined as
The chart below compares the li(N) function and the simpler approximation to the true number of primes less than or equal to N.
Gauss’s log integral approximation seems to overestimate the number of primes while the simpler approximation seems to underestimate them. By the time he was 70, Gauss had computed primes for the first 3 million numbers and li(N) had always overestimated the true number of primes. Gauss believed li(N) always would overestimate them, but he had no proof for that belief.
Gauss conjectured that the relative error between N/ln(N) or li(N) and the prime counting function would decrease as N became larger and larger. As we can see, the percentage error between li(N) and the true number of primes does indeed get smaller and smaller as N increases. This is the Prime Number Conjecture:
as x becomes larger and larger. The numerical evidence in the table below is very suggestive that’s it true but of course that’s not proof. The prime number conjecture could fail for much larger numbers.
It was Gauss’s student, Bernard Riemann, who made decisive progress in understanding the distribution of the prime numbers. Riemann began by studying theology, but Gauss recognized Riemann’s extreme mathematical talent and convinced him to switch to mathematics. Riemann made fundamental discoveries in complex analysis and non-Euclidean geometry and put the integral on rigorous foundation with Riemann sums. However, Riemann became most famous for the Riemann hypothesis, which came out of a short paper that Riemann wrote on the subject that had so long intrigued Gauss: how many primes are there less than a certain number? To understand what foundation Riemann built upon, we have to go back to Euler and the solution of the Basel problem.
The Basel Problem
The Basel problem was to find the sum of the reciprocal of all the squared natural numbers, i.e.,
The problem was named after the city of Basel, which was Euler’s and the Bernoulli brother’s hometown. The Bernoulli’s were not able to solve the problem, but Euler managed to do it around 1735. Euler’s solution is ingenious, leading to a solution not only to the original problem but also the to the sum of all reciprocals of the natural numbers taken to any even power.
To solve the problem, Euler started by writing the standard Maclaurin series for the sine function, which should be familiar from elementary calculus:
Any function can also be factored into a product of where its zero, providing an alternative way to write the function. For example, the function
and written in two way, since the function is zero at either x = 1 or x = -2. Since we know that sin(x) is zero at
we can write sin(x) in factored form as an alternative
Now let’s multiply this out, focusing on the cubic terms
If we equate the terms multiplying the cubic power of x in both the McLaurin series version of sin(x) and the factored form of sin(x), we get
or
From this relation, we can derive others that will prove useful later. Note that
and subtracting the equations
Also, we can see that
And finally, we can then get the sum of the alternating series:
Euler’s Product Formula
While he was working on the Basel problem, Euler realized that if he generalized it, writing it as sum to an arbitrary power of x, the new function, the ζ(x) function (zeta function), amazingly encodes all the primes. The ζ(x) function, a generalization of the Basel problem, is
For the zeta function, Euler derived closed-form solutions in terms of π for all even x: when x = 2, the sum is Π2/6. When x is 4, the sum is Π4/90 and when x is 6, Π6/945, and so on. The function is known to converge for all odd powers of x as well, although it is not known whether it converge to any nice formulas as the even powers do. However, the zeta function does not converge when x = 1, i.e., in that case it grows without bound, never approaching a particular value.
Since every natural number n can be written as a unique product of powers of primes, Euler noticed that ζ(x) could alternatively be written as
But each sum in the infinite product in the equation above is the sum of a geometric series. For example,
and
So, Euler showed that the zeta function can be written alternatively as a function of all the prime numbers.
Riemann’s Realization
Riemann realized from Euler’s work that the zeta function contains the secrets of the primes, which must hidden in the function somehow.
However, a look at Euler’s product function above presents a challenge. We know that this function converges to some non-zero value for all x > 1. The sum diverges for all x<=1. How does that help? It’s not at all clear how this function can tell us anymore about the primes than we already know.
Analytic Continuation Comes to the Rescue
Riemann was a master of complex analysis, the calculus of complex numbers. A complex number is a number a + ib that is a combination of a real part a and an imaginary part b, where
Riemann’s strategy to uncover the hidden structure of the primes in the zeta function was to generalize it to be a function of complex rather than real numbers. To denote that the zeta function is defined over complex numbers, we can change the argument x to s, where s is some complex number of the form s = a + ib. The new zeta function is then
If we do that, we have a complex-valued zeta function. It can be shown to converge for all s = a + ib for a > 1. For a <=1, the zeta function diverges. Unfortunately just extending to complex numbers doesn’t help much.
However, Riemann performed some mathematical wizardry, analytically continuing the zeta function so that it is defined over the larger domain of complex numbers that includes a <=1. To understand analytic continuation intuitively, it may be helpful to recall the parable of the three blind men trying to understand an elephant. One man can only feel the elephant’s trunk, and so thinks the elephant is the same as its trunk. Another man feels the elephant’s tail and thinks the tail is the elephant. The third man feels the elephant’s ears and thinks the ears are the elephant. The men need to find a way to piece together their limited observations of the elephant to understand what it is in its entirety.
Functions in the complex plane can behave the same way. We may see one form of a function over a limited domain of the complex plane. But that’s just a limited piece of a larger function that takes a different form over a broader domain of complex numbers. But it’s still the same function. Finding the analytic continuation of the zeta function is analogous to the blind men feeling different parts of the elephant and piecing them together.
Analytically Continuing the Zeta Function To Be Defined Between 0 and 1
We can extend the zeta function to a larger domain of complex numbers by defining the eta function
It can be shown that this function converges for all complex numbers s = a + bi, where a>=0 and a ≠ 1. Notice that
Solving for ζ(s)
We have found the more general zeta function that is defined over the larger complex domain s = a + bi in terms of the eta function, defined for a>=0 and a≠1. Originally, zeta was defined for a > 1 and now the extended version is defined for a >= 0, a larger domain.
Since η(s) is defined over that larger domain, this extended zeta function will give the same values as the original zeta function for a >1. For example, let’s use it to calculate ζ(2) which we already know to be Π2/6.
Plugging 2 into the extended zeta function, we see the extended zeta function agrees with the original zeta function.
The Zeros of the Extended Zeta Function
How does the extended zeta function help? Riemann deduced that the zeros of the extended zeta function, which are complex numbers that make the extended zeta function zero, amazingly determine where the prime numbers are. The extended zeta function has an infinite number of complex zeros in the extended strip
for all imaginary numbers b. These zeros are called the critical zeros. If we know the values of the critical zeros, we can determine where the primes are.
How Do We Find the Zeros of the Zeta Function?
There are many methods to calculate the zeros of the zeta function. For example, we can use the eta function to find the zeros of the zeta function. As the expression we already derived shows below, whenever the eta function is zero the zeta function will be zero as well, i.e, if η(s) = 0, then ζ(s) = 0.
So, we have reduced the problem to finding the zeros of the eta function. The eta function can be written as
Looking at the general term, we see that
Recall Euler’s relation
Then
Thus, we can write the eta function as
when the real and imaginary parts of η(s) equal zero. The eta function will be zero when the real and imaginary parts are both zero.
and
Notice also that if s = a + bi is a zero, then s = a – bi is also a zero. That’s because the sign of b doesn’t matter since, by properties of the sine and cosine
and
Thus, critical zeros of the zeta function always occur as complex conjugates.
The chart below graphs the zeros for the real and imaginary parts of the eta function. The red line is the graph of all the complex values in which the cosine terms sum to zero, and the blue line depicts all the complex values in which the sine terms sum to zero. Where they intersect is where both the real and imaginary components are zero, i.e., where the eta function is zero. The intersection of the curves defines the critical zeros. The chart below shows the first three critical zeros.
Riemann calculated the first few zeros of the zeta function by hand and noticed that the real part was ½ in each case. Riemann conjectured that all the zeros have real part equal to ½--that’s the Riemann hypothesis. To date, over 12 trillion zeros have been calculated and all of them have real part equal to ½. However, no one yet knows whether it’s always true that the zeros have real part equal to ½. We’ll explain why it’s so important to settle this question in the following sections, when we learn how the zeros determine where the prime numbers are.
More General Analytic Continuation: The Functional Equation
The zeros we found in the strip
are termed the “critical zeros.” There are also additional infinite zeros on the negative real axis called the “trivial zeros.” Given how we’ve extended the zeta function so far, we cannot see these zeros. However, Riemann found an even more general analytic continuation of the zeta function that is defined for all s = a + bi where a ≠ 1.
This general zeta function is written as
This equation is called the “functional equation” because it relates ζ(s) to ζ(1-s)
Using this equation, we can trivially see that ζ(s) also has zeros at s = -2,-4, -6, -8, …. besides the critical zeros we already found, since
All the zeros of the zeta function in the complex plane are depicted below.
How Many Primes Are There Less Than Or Equal to any Chosen Number?
Armed with knowledge of the zeros of the zeta function, Riemann was able to derive a formula that related the prime numbers to the zeros of the ζ(s) function. Let us define π(x) to be the number of primes less than or equal to x. Riemann derived the following formula for π(x)
where
The function η(n) is the mobius function. It takes on values of -1, 0, or 1 depending on what n is. Notice that the logarithmic integral li(x) appears in the formula, but in a more complex way than known to Gauss. The critical zeros appear in the formula as well, denoted as ρ. Each critical zero is the exponent of x in the li(x) function. If we take just one term in the infinite sum, n = 1, and drop the critical zeros summation term and both ln(2) and the integral in J(x), both of which are small, we can recover Gauss’s approximation discussed earlier.
since μ(1) = 1. Gauss’s approximation is therefore a special case of the Riemann formula.
To see how the zeros determine where the primes are, we can compare the true number of primes to Riemann’s formula using just 10 J(x) terms and either 10, 25, 50, or 100 zeros and their complex conjugates. Truncating Riemann’s formula implies that we are approximating where the primes are, but, as can be seen, even using just 50 zeros reproduces the true prime counting function very well.
A Better Way To Pick Out The Primes Using the Zeros of ζ(s)
About 35 years after Riemann, Hans von Mangoldt derived a simpler formula for the primes, a formula that is preferred in modern textbook treatments of the Riemann hypothesis. By looking not at the number of primes, but rather at the sum of the natural logs of the number of primes, von Mangoldt was able to produce a simpler formula. Let ψ(x) denote the sum of the natural logs of each prime or power of a prime less than x:
The function ψ(x) defines a step function like the prime counting function, with the difference that it pulses up by ln(p) for each prime or power of prime it counts. Von Mangoldt showed that this formula could be written as:
This function says that ψ(x) rises linearly with x, but then has some correction terms, with the most important being the last term, which depend on the critical zeros ρ. Although not obvious, the second to the last term arises from the trivial zeros. The term
actually depends on all the zeros, but the trivial zeros have been written separately in the formula, so that the ρ terms refer only to the critical zeros in Von Mangoldt’s formula. To see this, let’s take the summation term, but only include the trivial zeros in it, the negative even numbers. Then that summation term would be written as
We’ll prove that
The Maclaurin series of ln(1+y) is
If we substitute
we get
Thus, the infinite trivial zeros can be compressed into the simple expression
Picking Out the Primes
To show how we can use the von Mangoldt function to pick our the primes or power of primes, note that
The derivative of the von Mangoldt pulses whenever it encounters a prime or power of a prime but is zero otherwise. Thus, we can use the derivative of the von Mangoldt function to pick out where the primes are.
Taking the derivative of ψ(x), we get
This function will pulse at every prime or power of primes. We can write this formula more simply by taking one xρ-1 term in the sum and noting that every zero s = a + bi is matched by another zero that is its complex conjugate a - bi in the infinite sum. Taking as an example one critical zero a + bi and its complex conjugate a - bi, we see that
We can write
But we know that
and thus,
a simpler formula that makes clear the role of the the real part a and the imaginary part b of the critical zeros. The Riemann Hypothesis states that a is always 1/2 in the formula above.
The Music of the Primes
The last term in ψ'(x) is a series of waves. Let’s look at the equation for the wave resulting from the first critical zero 1/2 + 14.134i
It looks like this:
As we can see, the first zero defines a wave that goes out to infinity. Notice that its frequency slows down, since the imaginary component of the zero is multiplied by ln(x), which grows more slowly than x. The amplitude of the wave also gets smaller over time, at the rate 2/x1/2
The chart below depicts the wave produced by the 50th zero. We see the same pattern: the wave starts off with very high frequency, because of the constant 143.118 in the cosine term. However, the frequency slows down because the constant is scaled by ln(x). The amplitude of the wave also slows at the rate 2/x1/2
The essence of the Riemann hypothesis is that the amplitudes of all the waves slow down at exactly the same rate, 2/x1/2. That’s only possible if all zeros have real part equal to ½.
Mathematicians sometimes refer to the “music of the primes” because each wave created by the infinite imaginary parts of the zeros are playing at a different frequency, much like musical instruments emit sound waves at different frequencies. The waves of the zeta orchestra come together to create a symphony of the primes and powers of primes. However, if the Riemann hypothesis is true, all the zeta waves have the same amplitude at each point: none of the zeta instruments are playing any louder than any other. The amplitude of every wave slows down at exactly the same rate, 2/x1/2.
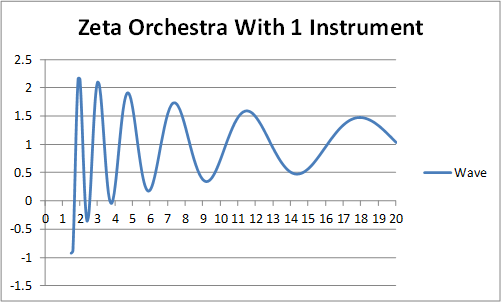
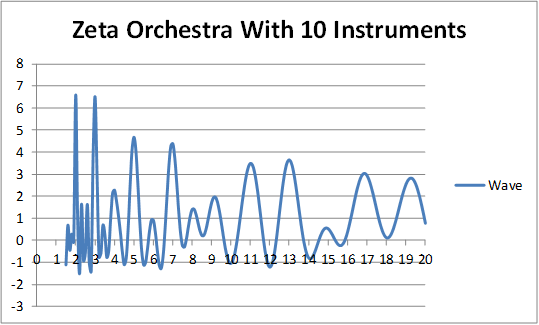
We can see how the zeta waves come together in a symphony, canceling each other out except where primes and powers of primes reside, by graphing them for different numbers of zeta zeros.
Suppose we use only the first zeta zero and its complex conjugate in the sum. No pattern emerges yet.
With ten pairs of zeros included in the sum, we still don’t see a clear pattern.
Using 50 pairs of zeta zeros in the sum, our orchestra seems to be picking out primes and powers of primes.
Let’s add more instruments to the orchestra to confirm, including 100 pairs of zeta zeros in the sum. One hundred pairs of zeros is enough to see the primes below 20 picked out.
Do the Trivial Zeros Matter?
We focused on the wave component of Mangoldt’s function, which depends on the critical zeros. It’s sometimes thought that the trivial zeros play no role, but, as we have seen, that’s not really true. As we will recall, the trivial zeros contribute the term
in Von Mangoldt’s formula. That term is very tiny however. At x = 2, it’s only 1/6 and becomes smaller and smaller as x increases. The effect of the trivial zeros is indeed trivial, but not zero.
Why Does the Riemann Hypothesis Matter For Pure Mathematics?
Using methods first developed by Riemann, mathematicians finally proved that the prime number conjecture was valid at the end of the 19th century. Recall that the prime number conjecture is that
as x becomes larger and larger. That means that the true number of primes less than x will get closer and closer to Gauss’s approximation li(x). However, the prime number conjecture doesn’t really pin down the structure of the primes precisely. There could still be pockets for very large x in which the density of primes suddenly increases and other regions where they become scarcer than expected. However, if the Riemann hypothesis is true, we can say precisely how good an approximation li(x) will be to the true number of primes less than x. The error between π(x) and li(x) will always be less than or equal to
if the Riemann Hypothesis is true. The following table shows highly tightly bound the primes are to the li(x) function if the Riemann Hypothesis is true.
The Quest Continues
The mathematician G.H. Hardy, working fifty years after Riemann, was obsessed with proving the Riemann Hypothesis. Besides mathematics, Hardy played cricket and real tennis (as opposed to lawn tennis) and was an expert in ball games. He believed in pursuing mathematics for its own sake, a philosophy he explained in “A Mathematician’s Apology”. Hardy proved that there are an infinite number of zeros of the zeta function that have real part ½ , but that of course doesn’t mean that all of them do.
Mathematicians continue their attempts to prove the Riemann Hypothesis. One empirical way to proceed is to calculate the zeros by computer. If one zero is found that has a real part not equal to 1/2, that would disprove the Riemann hypothesis. However, so far the Riemann hypothesis has been verified computationally for over 12 trillion zeros.
Like Hardy, pure mathematicians work on the Riemann Hypothesis for its own sake, not because there are necessarily any applications. However, the resolution of Riemann’s hypothesis will probably open up new vistas in mathematics, many of which may inspire new applications. Hilbert once said that if he woke up after 500 years, his first question would be to ask whether the Riemann Hypothesis had been proved. In his retirement address (and on his tombstone), Hilbert summed up the motivation of pure mathematicians and scientists by saying: “Wir mussen wissen, wir werden wissen”—We must know, we will know.