The General Solution to Camel Transporting Bananas

How many and what fraction

Problem: You may have seen examples of this problem on the internet. The usual way the problem is posed is the following:

You have 3000 bananas that you want to transport to a town 1000 kms away, using only a camel as the mode of transportation. The camel can carry a maximum of 1000 bananas at a time but eats one banana every km it travels while carrying bananas. If the camel is not carrying anything, he does not need to eat. What fraction of bananas can you transport?

The problem is not trivial because if you load up the camel with 1000 bananas each time, he will have eaten all of them by the time you get to the end of the journey.

Solution: We will solve this problem as it is usually posed and and then use it to find an exact solution to the general case where the camel can carry a load c, the distance to cover is d and the number of initial bananas is N = c x M. The questions we will ask are: How many bananas can be transported for finite N and what fraction of bananas can be transported in the limit when N tends to infinity?

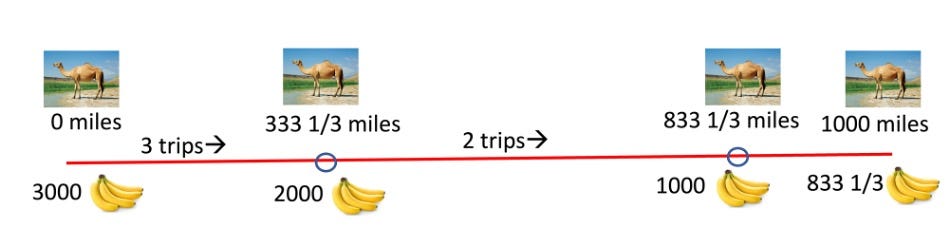
Let us illustrate the method using the problem as it is usually posed - there are 3000 bananas to transport to a distance of 1000 km, the camel can carry 1000 at a time but eats one banana for each kilometer if carrying bananas. If you just load the camel and go the whole distance, the camel will eat all the bananas by the time you get to your destination.

However, there is a better way. Let us divide the journey into two parts (see figure above). The camel first goes 333 1/3 miles three times with a load of 1000 bananas each time, depositing 666 1/3 bananas in each trip. This leaves 2000 bananas at a distance of 333 1/3 miles from the origin. The camel then goes another 500 miles twice, leaving 1000 bananas at a distance of 833 1/3 from the origin (or 166 2/3 miles from the destination). The camel walks the remaining 166 2/3 miles and consumes 166 2/3 bananas, leaving 833 1/3 bananas at the destination. The fraction transported is approximately 27.8 percent.

Asymptotic solution for a large number of bananas:

Let the number of initial bananas be N = 1000xM, with N, M very large. The camel carries a maximum of 1000 bananas. We load it up to its maximum capacity and make it walk 1000/M miles M times. In these trips the camel eats a total of 1000 bananas leaving 1000x(M-1) bananas at a distance 1000/M from the start. We repeat this by making the loaded camel walk a distance of 1000/(M-1) miles M-1 times. The camel again eats a total of 1000 bananas and leaving 1000*(M-2) bananas at a distance of 1000/M + 1000/(M-1) from the start. We repeat this process k times until we get as close as possible to the end of the journey. We now have moved a distance 1000*(1/M + 1/(M-1) + 1/(M-2) + …+ 1/(M-k+1)) miles and have left 1000*(M-k) bananas there. Since the total distance is 1000 miles, we need to make as close to 1000 as possible. Thus, we must have:

1000*(1/M + 1/(M-1) + 1/(M-2) + …+ 1/(M-k+1)) = 1000 or

(1/M + 1/(M-1) + 1/(M-2) + …+ 1/(M-k+1)) = 1.

The left-hand side can be written as H_M – H_M-k where H_M = 1 + 1/2 + 1/3 +…+1/M is the Harmonic series.

For large M,

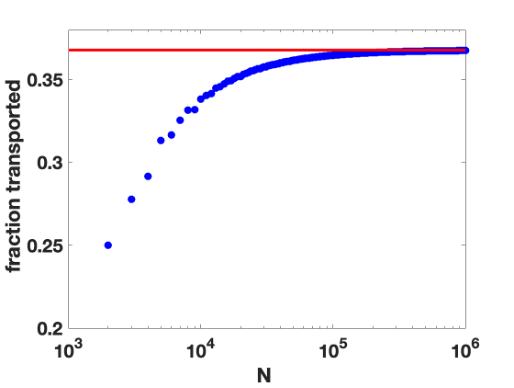
where is the Euler-Mascheroni constant ~ 0.57721. Neglecting terms that vanish in the large M limit, the equation to solve is then ln(M/(M-k)) = 1 or (M-k)/M = 1/e. Since the camel eats 1000 bananas for each trip, in k trips the camel will eat 1000*k bananas. This means that the fraction of bananas transported is 1000*(M-k)/N = (M-k)/M = 1/e. Hence, for a large number of initial bananas, the camel will transport a fraction 1/e of the bananas. It is simple to write a computer program to check this calculation. This is shown in the figure below with 1/e ~ 0.368 shown as a red line.

General Solution: Suppose the camel can carry a load c, the distance to cover is d and the number of initial bananas is N = c*M. The camel first goes M times to a distance of c/M with a load c of bananas. He eats c bananas and leaves c(M-1) bananas at a distance of c/M from the start. He repeats this going a distance c/(M-1), M-1 times; c/(M-2), M-2 times, … c/(M-k+1), (M-k+1) times with a full load. This leaves c(M-k) bananas a distance c * (H_m -H_m-k).

After k steps, the distance travelled will be:

(c/M + c/(M-1) + c/(M-2) + …+ c/(M-k+1)) which we want to approach d.

Thus, we must have:

(1/M + 1/(M-1) + 1/(M-2) + …+ 1/(M-k+1)) = d/c

or in the large M limit, ln(M/(M-k)) = d/c. As before, the fraction of bananas transported is (M-k)/M. Hence, the fraction of bananas transported in the limit as M becomes very large is e^-d/c.