Solution to Ramsey Theory - clique of size 3
In group of six people, three are friends or strangers
Ramsey theory is a branch of mathematics that looks for ordered subsets in random systems when they get large enough. The simplest problem in Ramsey theory is the following: What is the smallest number of people to guarantee a clique of size 3? A clique in this context is defined as a set of people who are either friends or strangers. To make the problem simpler, we will give the answer. A clique of size 3 is guaranteed among six people. The problem we will pose is to prove that this is true.
Prove that in a group of six people, there must be three people who are friends (know each other) or strangers (do not know each other).
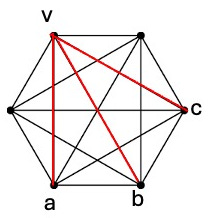
Solution: We will use the images below to prove this statement. Suppose we consider the people as vertices and relationship (friends or strangers) as links colored blue and red respectively. Pick a vertex. Since there are only two colors available, and there are 5 links out of v, at least 3 of them must be the same color. Let us choose this color as red (shown in image). Let us say that these links connect to vertices a, b and c. Now consider the triangle a, b, c. Since there are only two colors available, either one of the edges, there are only a limited number of possibilities to color them.
All are blue. But this would make a blue clique of size 3 from the triangle abc.
Two are blue and one, say ab, is red. In this case, we have the red clique vab.
Any other choice of colors with more reds would give at least one red clique of size 3.
This proves that with six people, there must be a clique of three people, who either all know each other, or all do not know each other.