Solution to Darwin’s Dilemma

The Hardy-Weinberg Theorem

The major idea at the center of all biology is evolution, discovered simultaneously in the mid-1800s by Alfred Russell Wallace and Charles Darwin. The terms “Natural Selection” and “Descent with Modification”, coined by Wallace and Darwin respectively, completely changed our views about life on earth. When Darwin formulated his theory about “Descent with Modification” and Wallace about “Natural Selection”, all of the biology of genes and chromosomes and how they influence inheritance was unknown. Neither did Darwin and Wallace know about the experiments of Gregor Mendel, the monk whose studies on peas and flowers showed that information from one generation to the next is transmitted in particulate form, which we now know is due to the way genetic information is coded in chromosomes. When Mendel crossed pure bred pea plants with purple and white flowers to study inheritance patterns, he found that in the first generation (F1) they produced only purple flowers. When the F1 purple flowers were self-pollinated, they produced both purple and white flowers in the ratio of 3:1, purple:white. This led him to propose that the purple flower color in peas was a “dominant” trait, while the white flower color was a “recessive” trait. He also observed that other traits, such as seed shape or size, were not linked to flower color. His main conclusions were that in peas, traits such as flower color, pea shape etc. are inherited in distinct patterns and do not blend. Each trait is determined by factors (now known as gene sequences) and each factor comes from each parent.

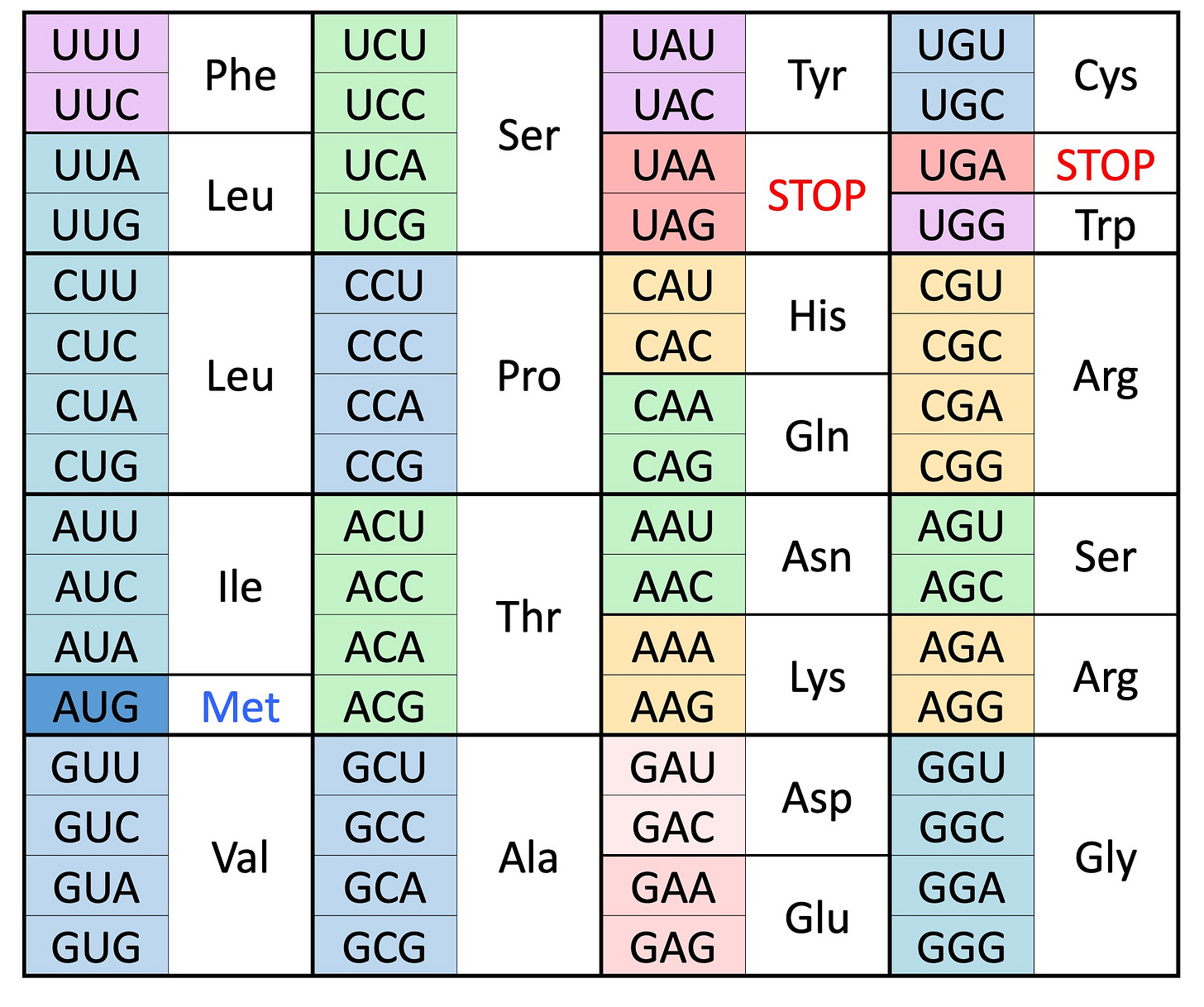
We now know that the information in cells is coded in long linear helical chains called chromosomes made by attachments of four elemental chemicals or bases – adenine, cytosine, guanine and thymine (shortened to A,C,G,T). The genetic information contained in the sequence of bases on chromosomes code for the twenty amino acids which make up our bodies. The translation of the message on chromosomes to amino acid chains is done in units of three bases (called codons) using a Universal Genetic Code. This is accomplished by a complex cellular machinery which requires that first the base T or Thymine be transformed into U or Uracil before it can be translated into the appropriate amino acid. The Universal Genetic code is shown in the figure above. It is degenerate, with multiple codons coding for the same amino acid. Thus, both UUU, UUC (or TTT, TTC) code for the amino acid phenylalanine. And CGU (or CGT), CGC, CGA and CGG all code for the amino acid Argenine. In addition, there are two stop codons to tell the machinery where in the sequence to stop and one start codon AUG (Methionine).

The mathematical basis of how traits are inherited and how Mendel’s experiments can be understood was discovered by Wilhelm Weinberg and independently by Godfrey Harold Hardy using notions of probability in what has become enshrined as the Hardy-Weinberg Theorem. We will assume that we are dealing with a species such as humans, where each chromosome comes in two copies. Such species are called diploid. Since there are two sequences coding for a given protein (one on each chromosome), they could either be the same or different. We call each sequence on the chromosome coding for a protein an “allele”. Each protein in an individual is then defined by two alleles (is bi-allelic) and these two together are referred to as the individual’s genotype at that chromosomal position (locus). We also assume that the population consists of a single isolated species in a fixed geographic area. Under the assumptions listed below, we will consider a bi-allelic locus with alleles A and a (note that here A and a just represent the coding sequence and not bases or amino-acids). We will try to understand how the genomes of such a population get transformed between generations using the following simplifying assumptions:

· We consider only diploid organisms (those that have two copies of each chromosome). Hence, an individual will have genotype either AA or Aa/aA or aa at the locus.

· Reproduction is sexual (as opposed to cloning).

· Generations do not overlap (clean break between parents and offspring)

· All loci are bi-allelic (i.e., there are two sets of paired chromosomes).

· No sexual dimorphism. Frequencies of alleles are the same in males and females – which means these arguments do not apply to sex-linked chromosomes, which do not always come in pairs. In humans, this means that the arguments below do not apply to the X and Y chromosomes in Males.

· Mating is random without selection for traits.

· The population size is infinite so we can talk about frequencies.

· There is no migration or mixing and no mutations (no changes in genetic sequence between generations).

· There is no allele specific selection (no benefit from having some specific allele).

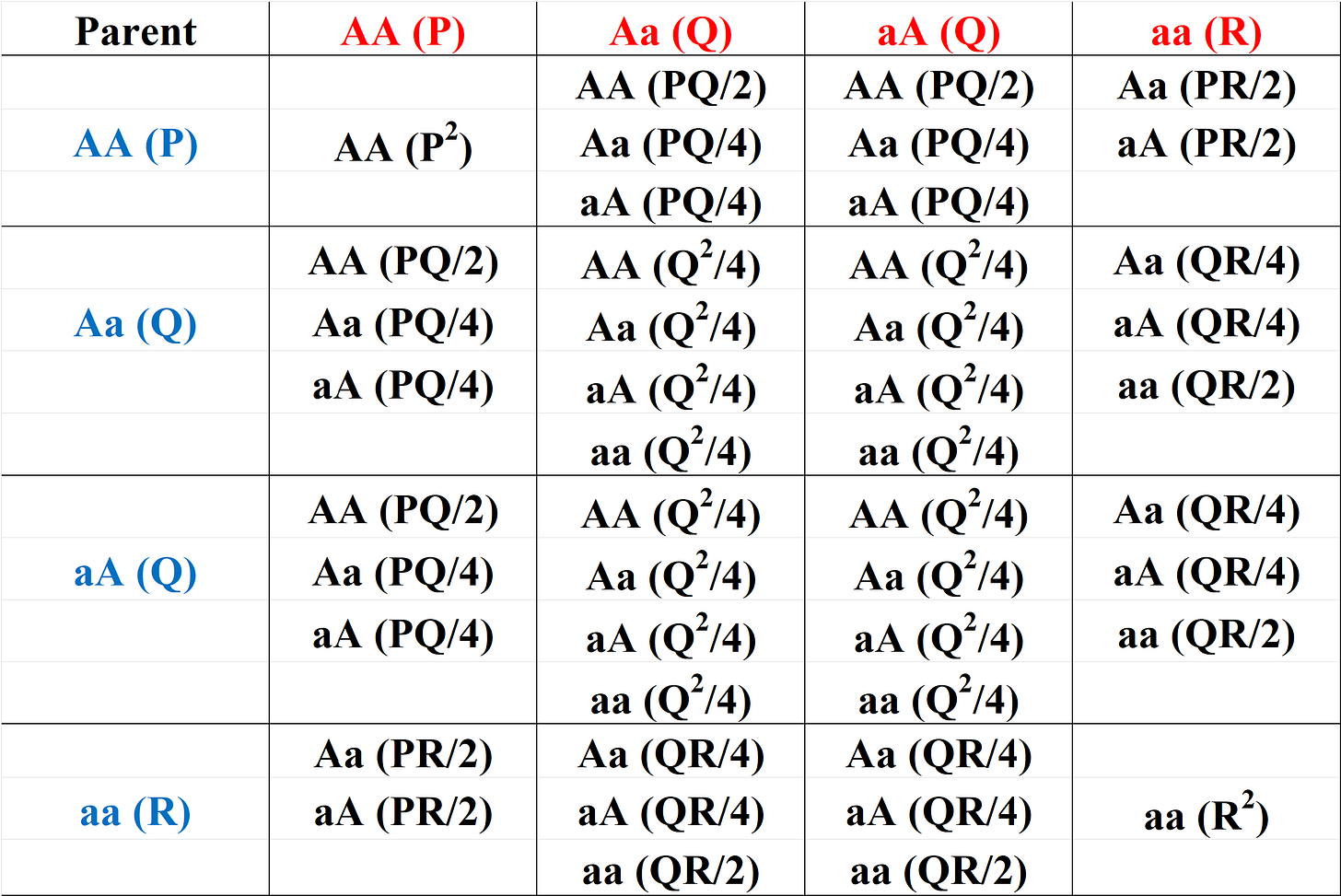
In the t th generation, let the individuals in the population have frequencies P, 2Q and R for the 3 possible genotypes: AA, Aa/aA, and aa respectively. These three genotypes are called homozygous wild type (AA), heterozygous Aa/aA and homozygous mutant (aa). By conservation of probability, P+2Q+R = 1. At time t+1, under random mating, the frequencies P’, 2Q’ and R’ of the three genotypes are given in the Table below. The parents are shown in the top row and first column, and each entry shows the resulting genotype(s) from the two parents along with its probability in brackets. The entries are obtained by looking at the row and column genotypes and finding all possible crosses. For example, crossing AA and Aa would result in equal amounts of AA, AA, Aa, aA or AA half the time and aA or Aa a quarter of the time. The probability of this cross in the population is PQ which is then split equally between these four possibilities.

The table above shows the frequencies in the next generation at time t+1 which are obtained by summing the cases which result in each of the three genotypes. Thus:

P’ = frequency of AA genotype at t+1 = P² + 2PQ + Q² = (P+Q)²

R’ = frequency of aa genotype at t+1 = Q² + 2QR + R² = (Q+R)²

Q’ = frequency of Aa genotype at t+1 = PQ + PR + QR + Q² = (P+Q)(R+Q)

Now consider what happens in generation t+2, with frequencies P’’, 2Q’’ and R’’ for the three genotypes. Using the same table but with P replaced by P’, Q by Q’ and R by R’, we have,

P’’ = (P’+Q’)² = [(P+Q)² + (P+Q)(R+Q)]² = (P+Q)² (P+2Q+R)² = (P+Q)² = P’ (since P+2Q+R = 1)

Thus, P’’ = P’. Similarly, we can show that R’’ = R’ and,

Q’’ = (P’+Q’)(R’+Q’) = [(P+Q)² + (P+Q)(R+Q)] [(R+Q)² + (P+Q)(R+Q)] = (P+Q)(R+Q)(P+2Q+R)²

= (P+Q)(R+Q) = Q’

Almost magically, the genotype frequencies became fixed after only one round of random mating. This is the Hardy-Weinberg theorem. It says that under the assumptions we made, genotypes in the population become fixed in one generation. Let p and q be the population frequencies of the “A” and “a” allele respectively. Since there are no mutations or migrations, these are fixed within our assumptions. In such a situation, the frequencies of the three genotypes AA, aA/Aa and aa would be p², 2pq, q² respectively. A locus where this is true is said to be in Hardy Weinberg Equilibrium.

It should be obvious that the Hardy Weinberg Theorem explains Mendel’s experiments succinctly. An allele “A” is said to be dominant over the allele “a” if it will force the expression of a phenotype (trait) in either the AA or the Aa genotype forms. A recessive allele is one which needs to be expressed on both alleles to show its phenotype. In Mendel’s experiment, the dominant purple color trait is coded in the AA or Aa/aA genotype while the white color is coded in the aa genotype. Offsprings of a pure cross AA and aa will be AA or Aa and always show the purple color, since it is a dominant trait. This means that , plants in generation F1 will be 50% AA and 50% Aa/aA. If these are then self-pollinated, the AA and AA cross will always have AA offspring with purple flowers. However, the Aa and Aa cross will have half expressing Aa (purple) and the other half expressing aa (white). Thus, on average across many experiments, we would get purple flowers (1 + ½) vs white flowers ½ the time or in the ratio of 3:1 purple to white.

The Hardy Weinberg Theorem is important because it resolves a criticism that Darwin had to contend with, which was the following: If phenotypic characteristics like color, height etc. are inherited from both parents, there should be an averaging effect over time – the so called “greying of the species”. After many rounds of random mating, everyone should become the same! However, this theorem shows that this cannot happen, because genotype frequencies (which determine traits or phenotype) remain fixed in a large, randomly mating population.

Some Consequences of the Hardy-Weinberg Theorem.

· A dominant allele will not spread. This is because the frequencies of the AA and Aa genotypes are fixed on average across the population, so the number of A alleles in the population are also fixed on average.

· A recessive allele a will never be lost even if the combination aa is lethal, so long as the heterozygous combination is viable and fertile. This is the case when P_aa = 0, P_Aa ≠0. Again, this is because the allele a will remain in the Aa genotype.

An example of such a situation is the case of Cystic Fibrosis (CF), a rare recessive disease caused by the presence of mutations in both copies of a single gene which codes for the CFTR protein (cystic fibrosis transmembrane conductance regulator). Among other serious problems, it causes frequent lung infections. The average life expectancy is between 37 and 50 years in the developed world and lung problems are responsible for death in 80% of people with this disease. The disease is most common in Northern Europeans and affects one in 2000 people. Thus, q² = 1/2000, which means, q = 0.02, p = 0.98 and 2pq = 0.04. This means that one in 25 people will have the mutation (be heterozygous for the disease) but will not be affected by it. The allele for the disease survives even though the homozygous mutant form is effectively lethal.

Suppose that the frequency of the “A” allele is p and of the “a” allele is q. Then the frequency of the AA, Aa, aa genotypes are p², 2pq and q² respectively. Since human females have two X chromosomes, the X linked genotype frequencies are in HWE in females but not in males, who have frequency p and q for the single allele A and a that they carry on their single X chromosome. If a recessive mutation on X causes disease then the disease will affect a fraction q² of females and a fraction q of males. The Male/Female disease susceptibility ratio is 1/q, which becomes large as qà0. Hence, the smaller the q, and the more likely it is to be mostly visible in males. Females are often carriers of X linked diseases and males are the sufferers. An example of an X linked disease in humans is Hemophilia, a disorder in which the blood does not clot properly and color blindness, both of which are much more common in males than in females.