Simpson's bias or Simpson’s Paradox is a statistical paradox first described by Edward H. Simpson (image above) in a 1951 paper titled “The Interpretation of Interaction in Contingency Tables.” This paradox may arise when making a decision either based on the global statistic over a set of numbers or using the same statistic over subsets of the numbers. The paradox is that the decision based on the global statistic is the opposite of the decision based on the statistic using subsets.
A classic case of Simpson’s Paradox is the Gerrymandering of voters by selectively redistricting to create a specific outcome. We will explain this with an example.
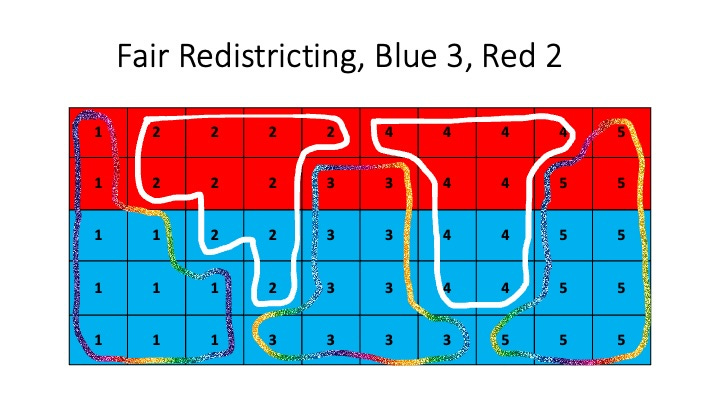
Consider the figure above which shows 50 voting districts. A red color represents voters who vote one way and blue who vote the opposite way. The group of 50 districts are to have five representatives based on division into five constituencies with one representative from each. A fair voting system would award three representatives to the blue districts and two to the red districts.
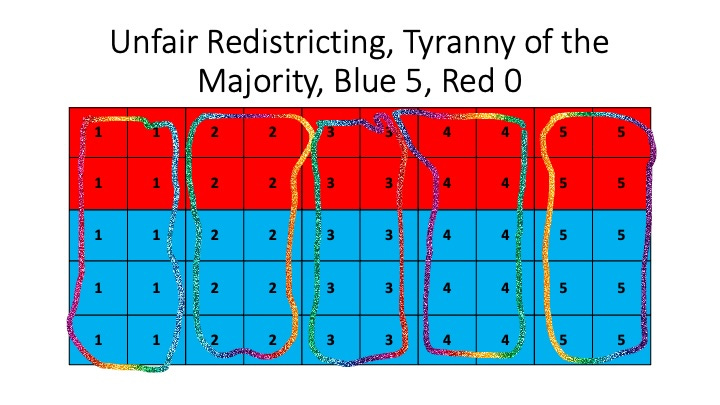
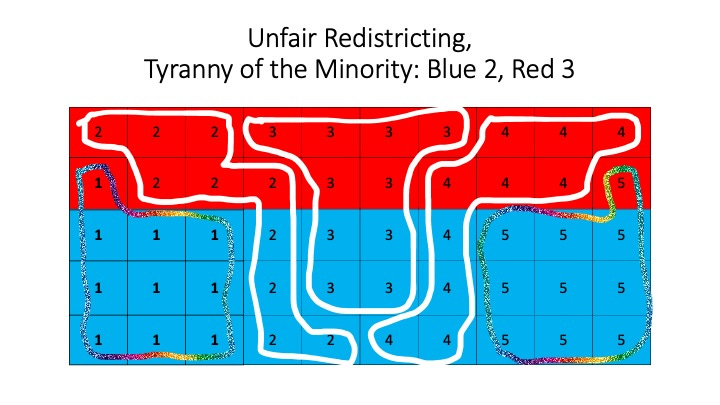
The figure above shows one possible fair division. However, it is also possible to group the districts into sets which would award all five to blue and none to red or the other way around.
This is shown in the two figures above and can be called the “Tyranny of the Majority” or the “Tyranny of the Minority.” These unfair ways of grouping illustrate Simpson’s paradox because the result is the opposite of what would be the outcome with representatives assigned based on the global voter distribution.