Playing A Fair Game of Craps with Loaded Dice

Solution

You and your friends want to play a game of craps, which requires two fair dice. The problem is that you have three dice, two of which are fair and one of which is loaded. You don’t know which of the dice are fair and which is loaded and you don’t know how the loaded die has been loaded. Is there a way to roll the dice to have a fair game of craps?

Solution: Choose two of the dice randomly and then discard the other. Roll the two selected dice once and take the sum mod 6. The value is the first fair dice roll. Then roll the two selected dice again, taking sum mod 6. The value is the second fair dice roll. For example, if you rolled a 1 and a 4 on the first trial, then the sum mod 6 is 5, so the first roll would be a 5. If on the second roll you got 3 and 6, then 3 + 6 mod 6 = 9 mod 6 = 3, so the second roll would be a 3. Therefore the roll is (5,3).

The reason this works is that either you chose the two fair dice randomly or you chose one fair die and one loaded die. If you chose the two fair dice, then rolling both and taking the sum mod 6 will be equivalent to one fair die roll. But if you chose one fair die and one loaded die, taking the sum mod 6 is also equivalent to one fair die roll.

To see this, let F be the value of the fair die roll and L be the value of the loaded die roll. Assume the loaded die has the following probabilities

\(P(L=j)=p_j\)

where

\(\sum_{j=1}^6p_j=1\)

Then

\(P(F + L=k\,mod\,6|L=j)=\frac{P(F + L=k\,mod\,6)}{P(L=j)} =\frac{\frac{1}{6}p_j}{p_j}=\frac{1}{6}\)

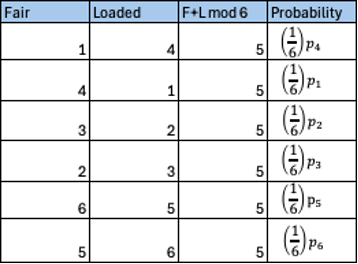
Another way to see this is to enumerate all possible ways to get a specific value. For example, the following table shows all the ways to get an outcome of five along with their associated probabilities.

Thus, the probability of rolling a five is

\(\frac{1}{6}p_1+\frac{1}{6}p_2+\frac{1}{6}p_3+\frac{1}{6}p_4+\frac{1}{6}+p_5+\frac{1}{6}p_6=\frac{1}{6}[p_1 +p_2+p_3 +p_4+p_5 +p_6]=\frac{1}{6}\)

The other possible outcomes can be readily verified.