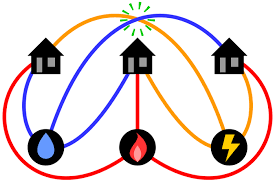
There is a famous problem (shown above) which is discussed extensively on the internet. It asks if it is possible to connect 3 houses to 3 utilities without the connection lines crossing. The answer is that this cannot be done. We will solve here the general case of n houses connected to m utilities and show that it is possible to connect them without lines crossing if and only if either m or n is less than 3.
The graph of n houses connected to m utilities is called a Kn,m bipartite graph. The K4,3 graph is shown in the figure. Assume the utility lines do not intersect, so the graph of the lines from the houses to the utilities is planar. We have shown that for planar graphs, Euler’s equation V+F-E=2 fit true (see here for the relevant post on this substack). Here we have V = (n+m) and E = nm. Applying the Euler formula, we get F = nm-(n+m)+2. Since there are no lines connecting houses or utilities, there are no faces with three sides. This means that each face must have at least 4 edges. Thus 4F is a lower bound for the number of edges. Each edge is connected to 2 faces so the total number of edges is 2E. So, we must have 4F ≤ 2E. This gives 4nm-4(n+m)+8 ≤ 2nm which simplifies to nm – 2(n+m) + 4 ≤ 0 or (n-2)(m-2) ≤ 0. This is only possible if either n=2 or m=2. Hence the Kn,m graph is planar if and only if either n=2 or m=2. In particular, connecting 3 houses to 3 utilities without lines crossing is impossible.