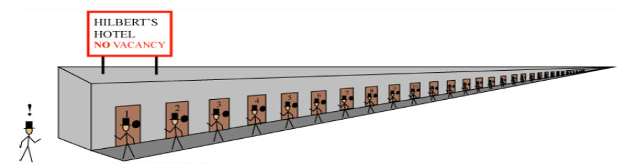
Infinity is a very strange beast. Here is how strange it can be (this is due to the German Mathematician David Hilbert (23 January 1862 – 14 February 1943)). We consider a hotel, which we can call Hilbert’s Hotel. It has an infinite number of rooms which are all occupied (No Vacancy sign outside).
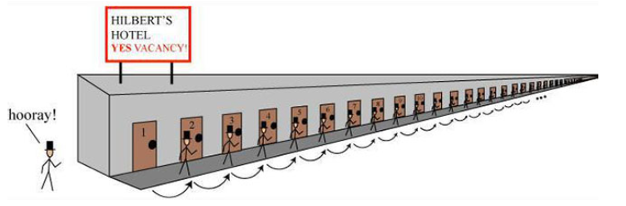
A VIP shows up and demands a room. The manager asks Hilbert what to do. No problem says Hilbert. He suggests they move the person in room 1 to room 2, the person in room 2 to room 3 and so on. The VIP can occupy room 1. This is shown below.
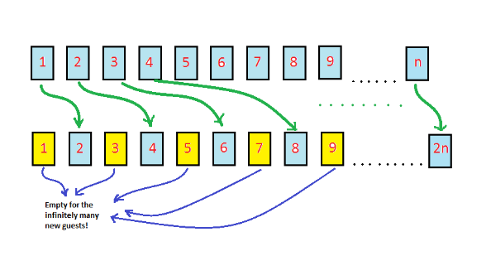
But what if an infinite number of VIPs show up and they all must have rooms? Again, it is very simple for Dr. Hilbert. Move all the guest in room k to room 2k. The odd numbered rooms will become empty, and the infinite number of VIPs can move into them. This is because the set of even integers is the same size as the set of integers. An infinite subset of an infinite set can be the same size as the whole set.
And finally, what if an infinite number of VIPs show up, each with an infinite number of attendants, and all demand rooms? No problem says Hilbert. Here is how it would work: Put the VIPs in Prime numbered rooms 2, 3, 5, 7, 11, 13,… Next, put attendants of the room 2 VIP in rooms 22, 23, 24… attendants of room 3 VIP in rooms 32, 33, 34,… and so on.
Interestingly there will be an infinite number of empty rooms after these transfers. Any room whose number is the product of two different primes will be empty. Examples: Room 15 = 3 x 5, Room 21 = 3 x 7, Room 35 = 5x7,.. etc. Even after giving rooms to an infinite number of VIPs, each with an infinite number of attendants, an infinite number of rooms remain empty! Infinity is indeed a queer beast.