A problem in Philosophy is the problem of Free Will: Are our actions predetermined or can we choose to do what we please. In 1960, William Newcomb, a physicist at Livermore Radiation Lab in California, posed the following problem:
Suppose there are two boxes which you cannot see into. Box # 1 contains $1000. Box # 2 contains either $1,000,000 or nothing. You have two choices:
Take both Boxes
Take only Box # 2
But there is a catch. Yesterday, a Supreme Being (SB) with predictive powers, made a prediction about the choice you would make. If she predicted you would take both boxes, she put nothing in the second box. If instead, she predicted you would take only Box #2, she put the $1,000,000 into Box # 2. If you use a coin toss to decide what to do, she left Box # 2 empty. What should you do?
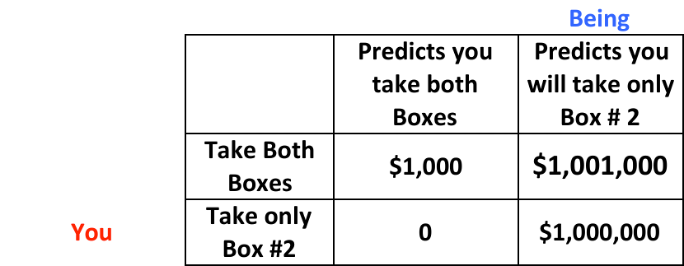
In the table above, we present this dilemma as a matrix game with the contents of the box as payoff. The SB has made her move (prediction and placement). What do you do?
What you do depends on what your belief system is. There are two ways to think about it.
Argument 1 (Believers): Suppose I take both boxes. Then the SB will have predicted I would do this and put nothing in Box # 2, so I will get $1000. If I take only Box # 2, the SB will have predicted this and put $1,000,000 into Box # 2. So I should take Box # 2.
Argument 2 (Non-Believers): The SB made her prediction yesterday and the money is already in the boxes. There is nothing the SB can do to change what is inside the boxes. If the $1,000,000 is in Box #2, it will not vanish if I take both boxes. So, I am better off taking both boxes, because even if the SB has not put the $1,000,000 in Box # 2, at least I will get $1000. So in either case, I should take both boxes.
Which Argument is correct depends on your level of belief. Suppose you think the SB is correct a fraction p times: The payoffs are :
A: both boxes: p x $1000 + (1-p) x $1,001,000 = $1,001,000 - $1,000,000 x p
B: only Box #2: (1-p) x 0 + p x $1,000,000 = $1,000,000 x p
Choice B is better than choice A unless p < 1,001,000/2,000,000 = 0.5005
How would you decide practically how often the SB is correct? You could watch 100 people play the game and record how often the SB made the correct prediction.
But you are a skeptic. You wish there was a way to see what was in the Boxes before you decided. Suppose the front of Box #1 was transparent and you could see the $1000 in it. However, the front of Box # 2 was opaque but the back was transparent and you had a friend who could see what was in that box. What would she tell you to do? But wait a minute! You already know what she would tell you to do. If there was nothing in Box # 2, she would tell you to take both boxes. If there was $1,000,000 in Box # 2, she would still tell you to take both boxes!
In either case, she would say “Take Both!” – you don’t benefit from her advice. You must decide for yourself!