How do we compare two sets to find out which one has a greater number of elements? Suppose you have two piles of apples. You want to know which pile has fewer more. One way to tell is to count the apples in each pile and compare the counts. The pile with the “greater” count has more apples. Another, seemingly equivalent method, is to repeatedly take one apple from each pile and put them aside. The pile that runs out of apples first has fewer apples. If both piles run out of apples at the same time, they have the same number of apples. At first sight, both these methods seem equivalent. However, this is only true if the number of apples is finite. If both piles have an “infinite” number of objects, then the final count in the first method is “infinity”. Unless we have a way to compare infinities, the counting option fails. However, the pairing method works just fine even for infinite sets.
This is the insight that inspired Georg Cantor (19 February 1845 – 6 January 1918) to develop a theory for infinite sets. Cantor was a German Mathematician and is considered the father of The Calculus of Infinities Although we naively use just a single symbol “∞” to represent any infinite quantity, Cantor and others after him showed that there are many infinities of different sizes, indeed an infinite number, of “infinities”. Mathematicians call the number of elements in a set the “cardinality” of the set. For instance, the “cardinality” of a pile of apples = the number of apples in the pile. Cantor invented a system to compare infinities. Here is the basic idea: We start with the set of all integers Z = {1,2,3,4…}. Mathematicians use the symbol Z for this set. We need one more definition to move on: A set is called “countably infinite” if its elements can be mapped one to one onto the integers (i.e. on to the set Z). By definition, the set Z is “countably infinite”. Following Cantor, we will use the symbol ℵ0 (or aleph-null) to represent the cardinality of the set Z. Thus, ℵ0 represents the “infinity” of the number of elements in the set of integers. The genius of the pairing method is that it allows us to find other sets with cardinality ℵ0. This can be done using Cantor’s Rule: Any set S whose elements can be mapped one to one onto the elements of Z has cardinality ℵ0. If there is no such mapping: i.e. if S has elements left over after all the integers have been used up, the cardinality of S is greater than ℵ0.
Let us consider some examples.
Consider the set E of all positive even integers: This is easy to map to Z. The E → Z mapping is, 2 → 1, 4→ 2, 6→ 3, etc. So, these two sets are of the same size and both have cardinality ℵ0.
Next, consider the set P of all prime numbers. We already know from an earlier post that P has an infinite number of elements. What is the cardinality of P? It is easy to see that the cardinality is ℵ0. This is because the prime numbers can be paired one to one with the integers. Thus, we can assign the integer 1 to the first prime number (the prime number 2), the integer 2 to the second prime number (the prime number 3), the integer 3 to the third prime number (the prime number 5) and so on. Since every prime number will thus be assigned a unique integer, with none left over, we have succeeded in a mapping P onto Z. By Cantor’s Rule, these two sets are of the same size and both have cardinality ℵ0.
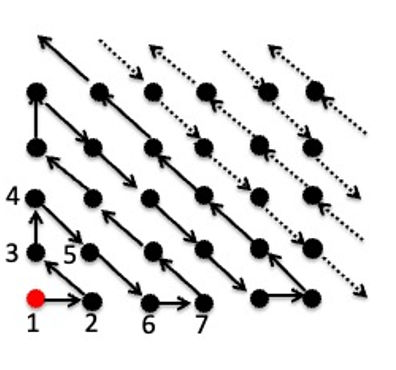
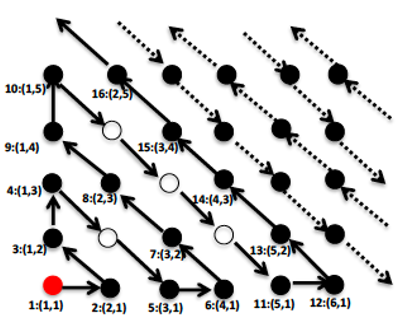
The set of points on a 2-d grid (see image above). Surely, you will say, there are more grid points in a 2-dimensional grid than the number of integers. Perhaps this set has cardinality greater than ℵ0. Alas, no. The elements of this set can mapped onto Z the integers (see image above). So, this set also has cardinality ℵ0.
How about the set Q of all rational numbers? Remember that a rational number is a number of the form p/q, where p and q have no common factor and q ≠ 0. Surely the cardinality of Q is greater than that of Z! Alas, Q also has cardinality ℵ0. Here is the proof:
Consider the figure above, where we have labeled the grid points by an integer as well as by two grid coordinates (n,m). The number n is called the x-coordinate. It is the horizontal distance of the grid point from the origin. The number m is called the y-coordinate. It is the vertical distance of the grid point from the origin. The quantity (x+y) is sometimes called the “Manhattan Distance” between the origin and (x,y), because it is the distance you would have to walk to get from O to (x,y) in Manhattan, New York City. Since the numbers n and m range over all the integers, the construction shown in the figure assigns the rational number (n/m) to each grid point. This proves that the cardinality of Q is also ℵ0. The acute reader may notice that we skipped some of the grid points (the ones shown as unfilled circles). This is to avoid mapping the same rational number to two different integers. For example, the point 3:(1,2) maps the integer 3 to the rational number ½. We then skip any grid point of the form (k,2k) for k=2,3,4,… since they would all represent the rational number ½. Indeed, in the figure above, we see that the grid point (2,4) is skipped. Similarly, all grid points (k,k) for k=2,3,4,… are skipped. They would all represent the rational number 1 = 1/1, which is already mapped at O as 1:(1,1).
You might be beginning to wonder if there are any sets which are not countable? Indeed, there are: Cantor’s showed that the set R of real numbers has cardinality > ℵ0. In fact the cardinality of just rational numbers in the closed interval (0,1) is greater than ℵ0..
Cantor’s Diagonal Argument: The set of Real numbers in (0,1) is uncountable.
Consider the set R of all real numbers between 0 and 1 written in decimal representation. Some of the elements of R have terminating decimal representations and others have non-terminating decimal representations. However, we can always write a terminating decimal as a non-terminating one by using an infinite sequence of 9s. For example, the terminating decimal number 0.1 can be written as 0.0999…. We will always use the non-terminating decimal representation. Suppose R is countable. Then there must be a way to label the elements of R using integers. Suppose that the following is one such representation:
R = {s1, s2, s3, s4, s5, s6, ….}, with
r1 = 0.1721612…..
r2 = 0.9212014…..
r3 = 0.0981345….
r4 = 0.4239190…..
r5 = 0.2959856…..
and so on. We will now construct a number r0 which is a member of R but is not in the list above. Here is how the construction goes: r0 differs from r1 in its first decimal digit, from r2 in its second decimal digit, from r3 in its third decimal digit and so on. For the mapping shown above, one possible value for r0 is: r0 = 0.345171…… Since r0 is an element of R but not in the list, we have a contradiction. If R is countable, no such r0 should exist. Hence R is uncountable and must have more elements than the set of integers. The cardinality of R is > ℵ0. Since this is a subset of the real number set, the set of real numbers is also uncountable.
Using similar beautiful and simple arguments, Cantor developed the theory of infinite sets. Among his many astonishing results was the proof that the cardinality of R is 2^ℵ0. He also showed that given a set with cardinality ℵi, one can construct a set with cardinality 2^ℵi. Hence, there is an infinite hierarchy of sets with increasing cardinalities. One of his most famous conjectures was the Continuum Hypothesis, which states that there are no sets which have cardinality strictly between ℵ0 and 2^ℵ0. In other words, it is impossible to find a set S such that ℵ0 < Cardinality(S) < 2^ℵ0. Cantor believed his hypothesis was true and tried very hard to prove it, with no success. Kurt Gödel showed in 1940 that the continuum hypothesis (CH for short) cannot be disproved from the standard Zermelo–Fraenkel set theory (ZF), even if the axiom of choice is adopted (ZFC). Paul Cohen showed in 1963 that CH cannot be proven from those same axioms either. Hence, CH is independent of ZF. Both of these results assume that the Zermelo–Fraenkel axioms themselves do not contain a contradiction, which assumption is widely believed to be true. These results seem to show that under very general axioms of set theory, it is not possible to either prove or disprove the Continuum Hypothesis. However, not all Mathematicians agree. The search for a proof of the continuum hypothesis or its refutation remains an active area of research, and the problem remains the first of Hilbert’s 23 outstanding unsolved problems in mathematics.
We end with a word of caution. The ideas presented here were highly controversial when they were originally developed by Cantor and for many years afterwards. To some extent they remain controversial today. To find out more, we recommend looking here and here and here. They have a lot of information and links to papers and books which will tell you more about this fascinating field. Indeed, if a set theorist were to meet God, probably the first question she would ask would be: “Is the Continuum Hypothesis true?”