A Short History of Numbers From Ancient Times to the Late Middle Ages
We still use a lot it
Most of what you learn about arithmetic in the first stages of mathematics is memorization. You memorize the multiplication table and the steps to divide one number into another. By the time you are ready to leave elementary school, you take for granted that there is only one way to write numbers and one way to do calculations with numbers. The message most people get after they have taken their first mathematical steps is that the way we do it in math is the way it’s done!
That message starts many people down the road to disliking mathematics. By the time you leave elementary school, you may well understand why each step you take to divide numbers makes sense, but you may also have come away with the belief that math is a body of rules that you have to memorize. And that’s just how it is. For many people, their first and most important impression of math is that it’s logical, but also boring and tedious. There is nothing creative or inventive about it.
That impression is very wrong. The way we write numbers today and do arithmetic is not just how it is. For most of history, people used different methods to write numbers. Because of the way they wrote numbers, the calculations that we can do easily today, even if tediously, were much, much harder for them, and in most cases impossible. We take it for granted that we can do arithmetic with pencil and paper. Without our modern method for writing numbers, however, people in earlier times couldn’t write out calculations. They had to use counting machines. In addition, before modern numbers were invented, people couldn’t write large numbers. Writing numbers in terms of multiples of ten might seem simple and commonplace today, but it took thousands of years for people to figure out the advantages.
From 1500 BC, the Babylonian system didn’t change essentially for about 3000 years until the late Middle Ages in Europe when modern numbers were developed. During that time, although the symbols used for writing numbers changed, no real improvements were made in the western world. The Greek mathematician Archimedes tried to fix the problem of not being able to write big numbers. In doing so, he came close to inventing modern numbers. But he missed the key step and no further improvements were made for almost 2000 years after that.
Studying the history of numbers, in which we compare the present to the past, helps us to appreciate what marvelous inventions modern numbers and arithmetic are. Arithmetic may be tedious, but the historical alternatives are much worse. Understanding the history also reminds us that mathematical ideas never came easily. The Greek philosopher Aristotle, Alexander the Great’s tutor, told his pupil that “there is no royal road to learning.” There isn’t. When you find yourself bewildered by some mathematical idea, maybe even arithmetic, you shouldn’t lose heart if it takes you a few minutes, a few hours, or even a few months to figure it out. When our ancestors, including the greatest mathematicians from antiquity, struggled to understand the same idea you might find perplexing today, it usually took them a few hundred years and sometimes even a few thousand years before they got it. It took 3000 years before modern ways of writing and calculating with numbers were developed.
Primitive societies didn’t need to count
Primitive societies didn’t need to count. They had only three numbers, one, two, and many. Primitive humans didn’t need to count higher than two since humans share with animals ‘number sense,’ an ability to recognize when something is missing. In the eighteenth century, the Abipones, a tribe of South American Indians whose language had only three numbers, could notice when a dog was missing from a huge pack of dogs. They didn’t need to count the dogs.
When primitive people did use numbers, they often didn’t distinguish the number of the things being counted from the things themselves. Fiji islanders say 10 boats are a ‘bola,’ 10 coconuts are a ‘koro,’ and 1000 coconuts are a ‘saloro.’ We can see the vestiges of our own primitive past in modern English when we don’t separate the number from the things counted. We still call two singers a duet, two oxen a yoke, and two partridges a brace. We also do the same for the ‘many’ number. We say a group of lions is a pride, and a group of crows is a murder. Nowadays, we think of numbers as being different from what they count, but that’s not how our ancestors saw it.
When societies needed to count, they usually used groupings of five, ten, or twenty
Once people’s daily lives became too complicated to use number sense, they started counting. Gradually, they added more numbers to their languages. Once the numbers got too big to just add another word for the next needed number, people took the next natural step: they started grouping when they counted. If you’ve ever needed to count a large number of items, such as pennies, you know it’s hard to do without getting confused and losing your place. So, you’ll usually count in groups. You might for example count in groups of 20 pennies. That way, you can look at the height of each group and use your number sense to see if all the pennies have been accurately counted.
When people started grouping to help them count larger numbers, you see groups of 5, 10, and 20 popping up in most societies. Some used different groupings of course, but grouping by 5, 10, and 20 was most common, because people would naturally count using their bodies. Five fingers are on one hand, so five is a common grouping. Ten fingers are on both hands, so ten is a very typical grouping. And we have 20 fingers and toes, so twenty is a grouping we often see too. In Native American languages, for example, groups of 5,10, and 20 were used most often. Today, the grouping has standardized to 10 in our numbers, but we can still see remnants of the past in counting by groups of twenty.
For example, in modern-day French, counting is by tens after the number 10, which is ‘dix’ in French. Twenty in French is ‘vingt.’ Thirty is ‘trente.’ In French, you keep counting by tens until eighty, when suddenly you say ‘quatre-vingts’—which means four twenties. In old French, counting by twenty was more prevalent but all that remains of that past in modern French are the numbers 80, four twenties, and 90, quatre-vingt-dix, or four twenties and ten.
Counting by 20 is still seen in English too. In the Gettysburg Address, Lincoln famously said ‘four score and 7 years ago.’ Because a score is 20 years, Lincoln was saying 87 years ago. Score comes from Old Norse, ‘skor,’ and means notch or tally. The word originated from the practice of shepherds counting sheep by twenties and then putting a notch or ‘skor’ on a stick for each group of 20 sheep. We use ‘score’ all the time today when we talk about ‘keeping score’ or when we ask ‘what’s the score?’
The Babylonian number system
Although 5, 10, and 20 were the most common groupings used when counting, there were important variations among ancient peoples that still matter today. About 3500 years ago, the Babylonians grouped by 60 when performing mathematical and astronomical calculations, using a system called the sexagesimal numbering system. The sexagesimal system was similar to the modern system we use that is based on grouping by ten, except the base for sexagesimals was 60. Even though 60 was the base, the Babylonian sexagesimals also used a grouping of ten for the integers. Integers up to 60 were written using combinations of symbols for 1 and 10.
Like our modern numbering system, sexagesimal numbers were expressed in place-value notation. The place of the digit indicated the power of 60 that should be multiplied by the digit. There was no symbol for zero and no decimal point. As a result, the value of numbers had to be judged by the context.
The Babylonian sexagesimals used cuneiform
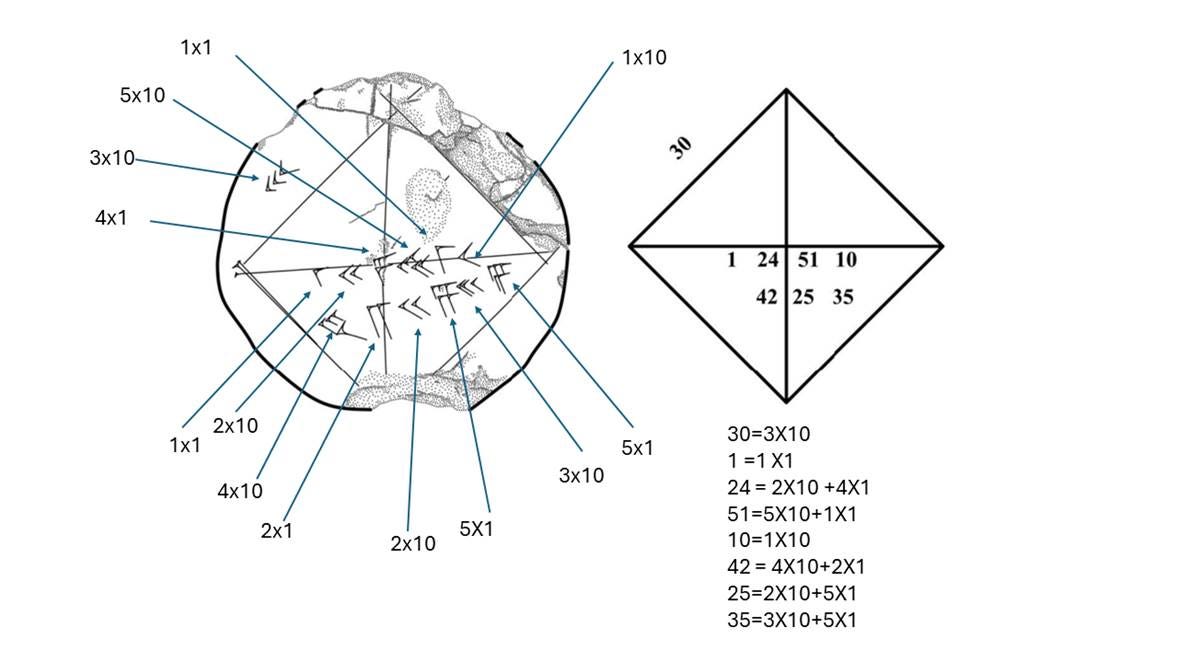
To see how sexagesimal numbers were written, we can look at the mathematical school clay tablet YC 7289, housed in the Babylonian Collection at the Yale Peabody Museum of Natural History.
The tablet depicts a square with two diagonals. On the side of one of the triangles bisecting the square is the number 30 in Babylonian cuneiform. Cuneiform is the system of writing used in some languages in the ancient Middle East. Written inside the square along the diagonal of the triangle are two further numbers. The diagram below shows how to decipher these numbers, which are very hard to read by modern standards.
The number 30, the length of the side of the square inscribed in the tablet, is written as three cuneiform symbols that represent 10 each. 3 X 10 = 30. The number 35, the last number on the lower right, is written as three symbols that represent 10 each plus five symbols that represent 1 each. 3 X 10 + 5 X1 = 35. Spaces between the symbols for counting the groups of ten and the symbols for counting groups of one separate the tens and ones places. Spaces also separate each full number. You read the numbers from left to right, starting with the tens place and then move to the ones place.
Since there is no symbol distinguishing the integer value of the number from the fractional part, such as the decimal point we have today, the Babylonians had to decide from the context if the number has a fractional part. On the tablet, some of the numbers represent fractions in a base 60 number system. For example, the sexagesimal number 1 24 51 10, the number on the diagonal of the square, should be very familiar to the modern mathematician. It’s a sexagesimal fraction in which the spaces between the last three numbers, 24, 51, and 10 indicate powers of 1/60. So, 1 24 51 10 should be understood as
If we write that out in decimal form, it’s 1.414213. To five decimal places, √2=1.4142135, showing that the number on the clay tablet is the square root of 2 written to surprisingly high accuracy. Just as a reminder of what the square root is, if you take the square root of any number, such as √x, and multiply it by itself, then (√x)2 = x So, (√2)2 = 2.
What do the other numbers mean. 42 35 25 is a sexagesimal fraction too:
But notice that
which is the second number on the Clay tablet. 42.4 is not exactly equal to the sexagesimal number 42.6 on the tablet because the Babylonian approximation to the square root of two is not as accurate as our modern decimal version.
An ancient tutorial on the Pythagorean theorem
The Clay tablet is actually an ancient mathematics lesson illustrating the Pythagorean theorem, which the Babylonians knew at least as early as 1500 BC. We’ll talk more about the Pythagorean theorem in the next chapter but for now we’ll state it: if you have a right triangle, then the sum of the squares of the sides equals the square of the hypotenuse. In terms of the Clay tablet, the sides of the right triangle are both equal to 30. That means the diagonal d can be written by the Pythagorean theorem as
Taking the square root of both sides, the diagonal equals
as the tablet showed.
The sexagesimal system was very advanced, allowing accurate computations for geometric and astronomical calculations.
How did the ancient Greeks write numbers?
The Greeks adopted a separate numbering system for everyday affairs and used the Babylonian sexagesimal system for mathematics and astronomy. The use of 60 in the Babylonian numbers is the reason the Greeks divided the circle into 60 parts and later Hipparchus, a Greek mathematician who is considered the founder of trigonometry, divided the circle further into 360 parts. That’s why a circle has 360 degrees today. We also have 60 minutes in an hour and 60 seconds in a minute for the same reason. The numbers 60 and 360 came to have special significance in ancient Greece and we see references to these numbers outside of mathematics. In the Odyssey, composed in the eighth century B.C., we are told that Eumaeus, Odysseus’s faithful swineherd, watches over 360 boars and 600 sows.
In ancient Greece, numbers for everyday use were based on the Greek alphabet rather than cuneiform. For example, the first letter of the Greek alphabet, Α, alpha, was associated with the number 1. The second letter of the alphabet, beta, Β, was the number 2. Each number from 1 through 9 was depicted by a letter from the alphabet. Separate letters were reserved for 10, 20, 30, and so on when counting by 10 from 10 to 100. Counting by thousands also had their own letters, with another letter reserved for 10,000. Ten thousand was called a myriad, a word we still use today to indicate a large number. The Greeks read numbers by adding up the value of each letter, subject to some other rules.
Problems with the Greek numbers
The numbering system used by the Greeks, and all numbering systems like it, had two practical problems. First, it was hard to write really big numbers, but the Greeks mostly didn’t need to write really big numbers. They thought there were magnitudes too big to count, such as the number of grains of sand in the world. The Greeks had a word that translates to ‘sand-hundred,’ which refers to an uncountable number. The 5th century B.C. poet Pindar in his second Olympian Ode said ‘the sand escapes counting.’
Perhaps more important, you couldn’t do arithmetic with pen and paper with the Greek numbering system. The arithmetic you learned in elementary school--addition, subtraction, multiplication, and long division--was too hard to do when everyday numbers were written as the Babylonians, Egyptians, Greeks, and other civilizations wrote them. Instead, people used counting boards, which were later called abacuses, to do arithmetic. Counting boards were simple devices that people used to count out the answer to an arithmetic problem using pebbles, beads or something similar. Finger counting, in which people did arithmetic on their fingers, was also in widespread from ancient times to the Middle Ages.
Archimedes figured out how to write really large numbers
Archimedes, one of the greatest mathematicians of the ancient world, challenged the belief that there were some numbers too big to count. In his short work, “The Sand Reckoner,” probably the first popular scientific article in history, Archimedes set out to prove to the King of Syracuse, using arguments the King could follow, that the number of grains of sand that could fill up the universe could be counted. To count the grains of sand that would fill up the universe, Archimedes adopted Aristarchus’s theory in which the sun is at the center and the earth revolves around it. The stars in the theory are like the sun, but at great distances away. Even in the third century B.C., many Greek mathematicians and astronomers had a pretty good idea of how the universe was constructed, knowledge that would be re-discovered in Europe over a thousand years later.
Because the number of grains of sand were so large according to Archimedes’ calculations, he had to invent new ways of writing large numbers. The traditional Greek number system would not work. He started with the myriad, which was 10,000 in the Greek numbering system, and multiplied it by itself, creating a new counting group of 100 million. He then created additional groups based on the myriad multiplied by itself again and again. Continuing in this way, Archimedes defined groups for counting as large as 80,000,000,000,000,000. Archimedes ultimately estimated that the universe, which he thought was a giant sphere, had a volume that could contain about 1063 grains of sand—10 multiplied by itself 63 times. That’s a very big number, but much too small an estimate given today’s astronomical measurements.
In building this new number system, Archimedes almost invented our modern number system. On the one hand, Archimedes demonstrated that number groupings can be as big as needed. If you start with a base grouping, the myriad, you could build up larger and larger groupings by multiplying the myriad by itself. That’s what we do today with the ten grouping. We keep multiplying 10 times itself to get larger and larger groupings—10, 100, 1000, and so on. When we write a number such as 245 today, we know that it means 2 X100 + 4X10 + 5 = 200 + 40 + 5 = 245.
However, Archimedes missed the other essential element of modern numbers, that a digit’s position in the number shows what counting group it belongs to. This is an odd oversight given the Greeks understood that the Babylonian sexagesimal system employed a place-value numbering system based on powers of the fraction 1/60. When we write the number 245 today, we mean that the 2 is in the hundreds counting place, so 2 means count two groups of one hundred or 200. The 4 is in the tens counting place, so 4 means count four groups of ten or 40. The 5 is in the ones place and so means count 5 things. This simple idea, which is so commonplace today, eluded even Archimedes, and was only re-discovered much later, in the 8th century A.D., a continent away in India.
The Roman numbering system took over from the Greeks
When the Romans conquered the world, they replaced Greek numbers with a number system similar to the Greeks but with different symbols. They counted in groups of 5 and 10. So, for example, I was 1, II was 2, V was 5, X was 10, L was 50, and C was 100. The Roman number system had the same problems as the Greek system: you couldn’t easily write large numbers and you couldn’t do arithmetic by hand using pen and paper. However, those problems didn’t prevent the Roman numbering system from being used throughout the Middle Ages.
The difficulty with writing large numbers wasn’t a big problem for most people during the Middle Ages. When numbers were used for everyday affairs, such as quoting prices, levying taxes, or measuring weights, Roman numerals could express large enough numbers. When merchants in the Middle Ages needed to do calculations, such as adding up costs and revenues from sales, they would do all the arithmetic on an abacus and then write down the final result in Roman numerals. For everyday calculations, no one had a great incentive to improve the number system. For calculations with fractions, mathematicians and astronomers continued to use the sexagesimal system adopted from the Babylonians until the late Middle Ages.
Although the Roman numerals and sexagesimal fractions were replaced in the late Middle Ages, some ancient number groupings besides 60 and 360 still survive. The Egyptians divided the day into 10 parts but reserved a twilight period in the morning and a twilight period in the evening, making 12 in all. They divided the night hours into 12 also, based on observations of stars. That’s why we have 12 hours in the day and 12 hours of night. The Egyptians also divided the year into 12 months.
The number seven is an additional important grouping that originated in ancient times. The Babylonians revered the number seven, since it was the number of the sun, the moon, and five planets they could see without a telescope. Veneration of seven was passed down by the Babylonians, making its way into the Old Testament. The Book of Genesis advised that God created the world in 6 days and on the seventh day he rested. Ultimately, that’s why we have a seven-day week.